An updated version of this article is available at https://mlengineer.substack.com/p/encoding-cyclical-features-for-deep-learning
Many features commonly found in datasets are cyclical in nature. The most common of which are time attributes: months, days, weekdays, hours, minutes and seconds all occur in specific cycles. Other examples might include features such as seasonal, tidal or astrological data.
A key concern when dealing with cyclical features is how we can encode the values such that it is clear to the deep learning algorithm that the features occur in cycles. This is of particular concern in deep learning applications as it may have a significant effect on the convergence rate of the algorithm.
This post looks at a strategy to encode cyclical features in order to clearly express their cyclical nature.
A complete example of using the encoding on weather data, which includes illustrating the effect on a three layer deep neural network, is available as a Kaggle Kernel.
The Problem with Cyclical Data
The data used below is hourly weather data for the city of Montreal. A complete description of the data is available here. We will be looking at the hour attribute of the datetime feature to illustrate the problem with cyclical features.
data['hour'] = data.datetime.dt.hour
sample = data[:168] # the first week of the data
ax = sample['hour'].plot()
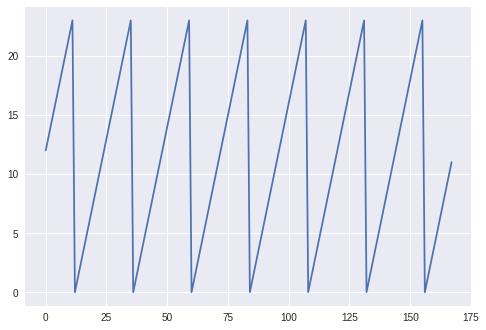
Here we can see exactly what we would expect from an hour value for a week: a cycle between 0 and 24, repeating 7 times.
This graph illustrates the problem with presenting cyclical data to a deep learning algorithm: there are jump discontinuities in the graph at the end of each day when the hour value overflows to 0.
From 22:00 to 23:00 one hour has passed, which is adequately represented by the current unencoded values: the absolute difference between 22 and 23 is 1. However, when considering 23:00 and 00:00, the jump discontinuity occurs, and even though the difference is one hour, with the unencoded feature, the absolute difference in the feature is of course 23.
The same will occur for seconds at the end of each minute, for days at the end of each year and so forth.
Encoding Cyclical Features
One method for encoding a cyclical feature is to perform a sine and cosine transformation of the feature:
$$x_{sin} = \sin{(\frac{2 * \pi * x}{\max(x)})}$$
$$x_{cos} = \cos{(\frac{2 * \pi * x}{\max(x)})}$$
data['hour_sin'] = np.sin(2 * np.pi * data['hour']/24.0)
data['hour_cos'] = np.cos(2 * np.pi * data['hour']/24.0)
Plotting this feature we now end up with a new feature that is cyclical, based on the sine graph:
sample = data[:168]
ax = sample['hour_sin'].plot()
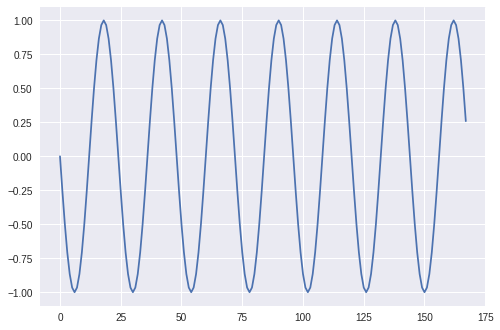
If we only use the sine encoding we would still have an issue, as two separate timestamps will have the same sine encoding within one cycle (24 hours in our case), as the graph is symmetrical around the turning points. This is why we also perform the cosine transformation, which is phase offset from sine, and leads to unique values within a cycle in two dimensions.
Indeed, if we plot the feature in two dimensions, we end up a perfect cycle:
ax = sample.plot.scatter('hour_sin', 'hour_cos').set_aspect('equal')
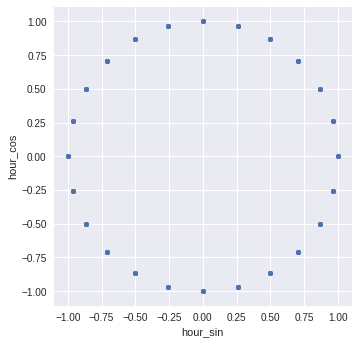
The features can now be used by our deep learning algorithm. As an added benefit, it is also scaled to the range [-1, 1] which will also aid our neural network. A comparison of the effect of the encoding on a simple deep learning model is given in the Kaggle Kernel.
Summary
Other machine learning algorithms might be more robust towards raw cyclical features, particularly tree-based approaches. However, deep neural networks stand to benefit from the sine and cosine transformation of such features, particularly in terms of aiding the convergence speed of the network.