Super-convergence in deep learning is a term coined by research Leslie N. Smith in describing a phenomenon where deep neural networks are trained an order of magnitude faster then when using traditional techniques. The technique has lead to some phenomenal results in the Dawnbench project, leading to the cheapest and fastest models at the time.
The basic idea of super-convergence is to make use of a much higher learning rate while still ensuring the network weights converge.
The is achieved by through use of the 1Cycle learning rate policy. The 1Cycle policy is a specific schedule for adapting the learning rate and, if the optimizer supports it, the momentum parameters during training.
The policy can be described as follows:
- Choose a high maximum learning rate and a maximum and minimum momentum.
- In phase 1, starting from a much lower learning rate (
lr_max / div_factor, wherediv_factoris e.g.25.) gradually increase the learning rate to the maximum while gradually decreasing the momentum to the minimum. - In phase2, reverse the process: decrease learning rate back to the learning rate minimum while increasing the momentum to the maximum momentum.
- In the final phase, decrease the learning rate further (e.g.
lr_max / (div_factor *100), while keeping momentum at the maximum.
Work from the FastAI team has shown that the policy can be improved by using just two phases:
- The same phase 1, however cosine annealing is used to increase the learning rate and decrease the momentum.
- Similarly, the learning rate is decreased again using cosine annealing, to a value of approx. 0 while momentum increasing to the maximum momentum.
Over the course of training this leads to the following learning rate and momentum schedules:
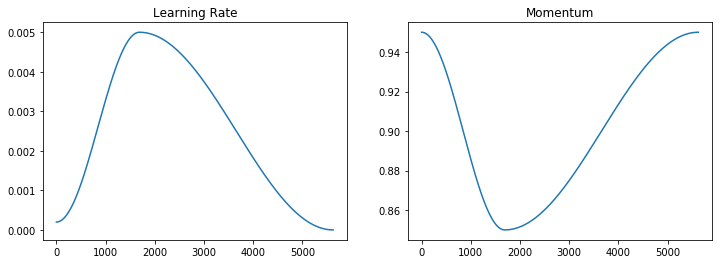
For a more in depth analysis of the 1Cycle policy see Sylvain Gugger's post on the topic.
Tensorflow 2 implementation
The policy is straightfoward to implement in Tensorflow 2. The implementation given below is based on the FastAI library implementation.
Application
Applying the 1Cycle callback is straightforward, simply add it as a callback when calling model.fit(...):
epochs = 3
lr = 5e-3
steps = np.ceil(len(x_train) / batch_size) * epochs
lr_schedule = OneCycleScheduler(lr, steps)
model = build_model()
optimizer = tf.keras.optimizers.RMSprop(lr=lr)
model.compile(optimizer=optimizer, loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(train_ds,epochs=epochs, callbacks=[lr_schedule])Results
For a complete example of how the 1Cycle policy is applied, including how to find an appropriate maximum learning rate, to two CNN based learning tasks, a Kaggle notebook has been made available.